Presburger arithmetic (also known as Linear Integer Arithmetic) is the first order theory of the naturals with addition and order. Quantifier free formulas of Presburger arithmetic look like this:

2x − y ≤ 2 ∧ x + y ≥ 4

Presburger formulas can be converted into deterministic finite automata that encodes their solutions.

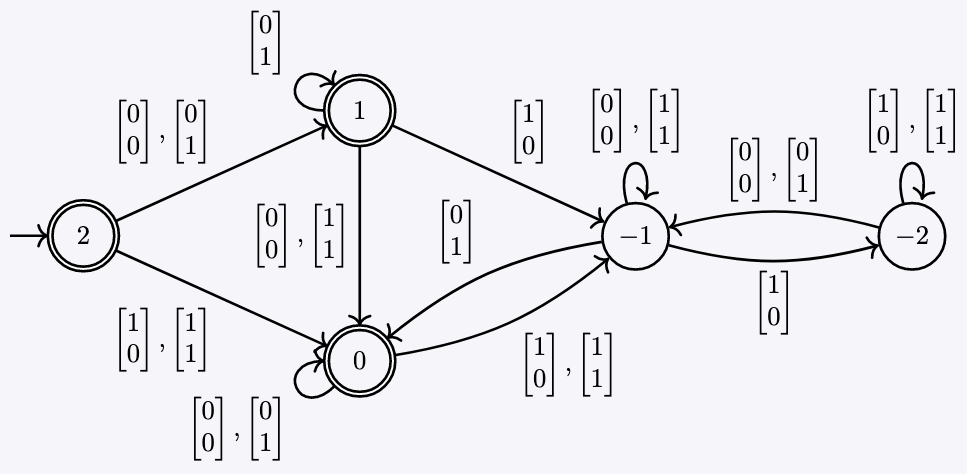
For example the following is the automaton for 2x − y ≤ 2.

These automata can get unpredictably large even for simple formulas.

A tool for computing lower bounds

We have developped a tool called Patapsco (Presburger Arithmetic to Automata Prober of State Complexity) that does not compute the automaton but instead provides a lower bound on its number of states. Patapsco is available at github.com/nicolasAmat/Patapsco. For more details see our paper.

🏆 The challenge 🏆

Help us! We already have computed lower bounds for many formulas but with your effort they could be vastly improved. If you think this challenge is for you then click ★ here ★.

Contact

For any questions, requests or suggestions please contact us at patapsco@imdea.org